聚焦2008北京奥运
《科学新闻》发文“泡泡组成的建筑”-鸟巢的几何结构
(转自科学新闻)
A building of bubbles
By Julie Rehmeyer,July 19th, 2008
The swim center for the Olympics,
which looks like it formed out of froth, was designed using the mathematics of
foam.
WATER CUBEMath
Trek: The National Aquatics Center in
The
But of course, those bubbles hardly skittered there of
their own free will. Creating this frothy confection took a lot of steel, a lot
of manpower, and not least, a lot of fancy mathematics.
SWIMMING IN BUBBLESThe
roof is constructed in the same manner as the walls.©Arup+Ben McMillan
The motivating idea for the building was that it would
express the spirit of water. Its designers first thought of liquid water,
vapor, or ice, but finally settled on foam. The bubbles, they decided, really
would be bubbles: pillows made of a transparent plastic called ethylene tetrafluoroethylene (or ETFE )
filled with air, attached to a steel framework outlining the edge of each
bubble.
A basic challenge was that they wanted the foam to look
random and organic. But for the engineering to be practical, it had to have
some underlying order. So Tristram Carfrae, an engineer at Arup, the Australian engineering
firm on the project, looked into the mathematics of foam.
KELVIN'S CREATIONKelvin's
"tetrakaidecahedra" create a foam structure
with very little surface area.K. Brakke
The trail led all the way back to an idea from the 1880s.
The physicist Lord Kelvin decided that the ether, the mysterious substance then
believed to fill the universe and transmit light waves, must consist of foam.
George Darwin (Charles’ son) declared the idea “utterly
frothy,” but Kelvin was undeterred. He set out to understand the shape that
ether-foam must have. The fundamental thing keeping bubbles together, he
realized, is surface tension, which tends to pull bubbles into a shape with the
least surface area for the volume. That’s why a single bubble forms a sphere.
The same principle determines the complicated shapes bubbles form when they are
packed together.
THE MINIMAL FOAM?The blue cells in this Weaire-Phelan
foam are dodecahedra, and the remaining cells each have 14 sides. K. Brakke
He also figured that the individual bubbles in the ether
were probably all of the same (very small) size. So the structure of the
ether-foam would be one with equal cell size and minimal surface area. But what
bubble shape created those properties?
It turned out that Kelvin was asking a hard question
indeed — so much so that it’s still unsolved and has been dubbed the “Kelvin
problem.” But Kelvin didn’t know that, and he set to work in the most
straightforward way possible: he started blowing bubbles with soapy water.
Before long, his experimentation paid off with a candidate shape he dubbed the
“tetrakaidecahedra.” It’s a modified octahedron, with
each sharp point sliced off and the edges and faces slightly curved. Kelvin
guessed, but couldn’t prove, that by packing these shapes together, he had
created the foam with least surface area for a particular bubble size — and
hence, perhaps, found the structure of the ether.
ANGLED CUTTo
get a natural-looking pattern of bubbles, Carfrae
sliced through the foam at an angle of about 111 degrees.Arup
He was wrong about the ether — not because it wasn’t
foam, but because it didn’t exist at all. But when Carfrae
read about this, he figured it was just what he needed to solve his engineering
problem: a systematic way to build foam.
Carfrae created a large block of Kelvin’s foam on a computer and tried slicing it
up, cutting at various angles to produce a flat surface he could use for his
walls. The result, however, didn’t look right. When he cut at some angles, the
bubbles were too regular. Other angles produced too many rectangular bubbles,
which just didn’t look real.
CELLULAR SKELETONThe
steel skeleton of the Weaire-Phelan foam structure
continues between the inner and outer wall surfaces. ©Arup+Martin
Saunders
Kelvin’s work did not solve Carfrae’s
problem. Kelvin’s work did inspire an entire branch of mathematics that Carfrae could mine for ideas. Mathematicians were stuck on
the small fact that Kelvin hadn’t proven his structure was the single
best. Could some other foam structure be lurking out there with even lower
surface area?
It took more than a century, but finally two physicists,
Denis Weaire and Robert Phelan of
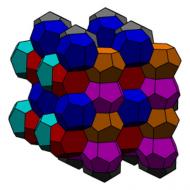
Unlike Kelvin’s structure, the Weaire-Phelan
foam was built from two different shapes. One was a slightly curved
dodecahedron and the other was a 14-sided shape with two opposite hexagonal
faces and 12 pentagonal faces. Despite the different shapes, Weaire made sure all the bubbles had the same volume. The
resulting surface area was a whopping 0.3 percent less than that of Kelvin’s
foam.
Weaire and Phelan are convinced that their solution is the best one, but, just
like Kelvin, they haven’t been able to prove it. Weaire
says that at this point, a proof would be extraordinarily difficult. “I’m not
holding my breath.”
Carfrae didn’t need a proof, though. He just needed the foam. He tried his same
slicing method using the Weaire-Phelan foam. This
time, by cutting at an angle of about 111 degrees, he found a pattern that
looked entirely natural. In fact, the pattern actually repeated in ways that
were very hard for the eye to detect. That repetition was key,
because it meant the building would be far easier to construct.
The Weaire-Phelan foam provided
not just a pretty surface for the walls, but the building’s very structure.
Imagine an enormous block of the foam, with steel beams outlining the edge of
each bubble. Now carve out the center to form a building with 12-foot-thick
walls and 24-foot thick ceilings. This is the weight-bearing structure of the
Water Cube.
The result is so strong, the engineers say, that the
entire building could be turned on its side without collapsing. Furthermore,
the remarkable effect is that they’ve designed a building without triangles.
Ordinarily, buildings rely on triangles to provide stiffness, since a triangle
is the only two-dimensional shape that can’t be deformed without changing the
length of its sides. The engineers say that this lack of triangles will make
the building more flexible and hence more able to withstand earthquakes.
To form the outside of the walls and ceiling, the
designers placed ETFE pillows in the polygonal openings created by the steel
beams. This created the three-dimensional, bubbly surface they were looking
for. They did the same thing for the interior walls. The empty chamber between
the interior and exterior walls provides solar heating and cooling.
Weaire learned of the building only after the design was complete, and he
visited the building during construction. He has two words to describe it:
“It’s spectacular.”