陈省身 － 积分几何与欧式微分几何
(转自《中国现代数学家传》)
R.帕勒 滕楚莲
作者简介 R．帕勒(Richard Palais)1931年出生于美国麻省凌县(Lynn，Massachusetts)．哈佛大学博士(1956)．现为勃朗蒂(Brandeis)大学教授．
滕楚莲（Chuu-Lian Terng） 1949年出生于台湾花莲．美国勃朗蒂大学博士(1976)．现任美国加州大学教授．
本文的材料主要取自：《陈省身论文选集》(S．S．Chern，Se-lected papers，vol．1—vol．4，Springer-Verlag，1978—1989)；《陈省身文选——传记、通俗演讲及其它》(科学出版社，1989)；以及作者与陈省身本人的多次谈话．文中，记号[1—25]，[1—30]等分别表示文献中所列的陈省身的出版物的序号．
陈省身
积分几何
Rn的刚体运动群G可迁地作用在各种各样的几何对象组成的空间S上(例如：点、直线、有某一固定维数的仿射子空间、有固定半径的球面，等等)，所以S可以看作一个齐性空间G/H，G上的不变测度诱导出S上的一个不变测度，此即首先由庞加莱(J．H．Poincarè)引进的“运动学密度”．积分几何的基本问题是将各种几何上有意义的量关于运动学密度的积分用已知的积分不变量表示出来(参看[1—84])．最简单的例子是关于平面曲线C的克罗夫顿公式：
∫n(l∩C)dl=
其中n(l∩C)是平面上的直线l与C的交点数，dl是直线组成的空间的运动学密度，L(C)是C的长度．此公式可解释为平面上直线与一条曲线相交的平均次数是C的弧长的两倍．
在[1—18]中，陈省身为广义的积分几何奠定了基础．A．韦伊在评论这篇文章时说：“它把布拉施克学派的工作一举推进到更高的水平．我对文章所显现的非凡才能和深刻见解有极深的印象．”在该文中陈省身首先把经典的“关联”概念推广到同一个群G的两个齐性空间G/H，G/K，设aH∈G/H，bK∈G/K，若aH∩bK≠
，则他称aH和bK是关联的．这个定义在蒂茨(J．Tits)的厦(building)理论中起重要作用．
在[1—48]和[1—84]中陈省身分别得到了Rn中两个子流形的基本运动学公式．陈省身的公式中用到了韦尔的管体积公式中的积分不变量．设Tρ是Rn中围绕k维子流形X的半径为ρ的管，则
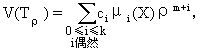
的李代数上的伴随不变多项式，Ω是关于X上的诱导度量的曲率张量．陈省身的公式是(同时由费德勒[H．Federer]独立发现)
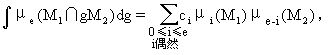
其中M1、M2分别是Rn中的p维、q维子流形，e是偶数，0≤e≤p+q-n，ci是依赖于n，p，q，e的常数．
格列菲思在评论陈省身关于积分几何的工作时说：“陈省身的证明显示了许多典型的特征．当然，一是用活动标架……另一个特征是通过直接的计算，而非建立一个复杂的概念框架；事实上，仔细观察会发现，确实存在一个如[1—18]所描述的框架，然而陈省身并未将它孤伶伶地提出来，而是让读者通过做一个不太简单的问题来理解它．”
欧氏微分几何
经典微分几何的一个主要课题是研究欧氏空间中子流形在刚体运动群作用下的局部不变量，即子流形的等价问题．这在30年代已经解决了．实际上，子流形的第一、第二基本形式Ⅰ、Ⅱ以及子流形的法丛上的诱导联络
0满足高斯、科达奇、里奇方程，且它们构成Rn中子流形的完全不变量组．具体地说，这些不变量是：
a)Ⅰ是在M上的诱导度量．
b)Ⅱ是M上在法丛ν(M)中取值的二次型，设u是在点p的单位切向量，ν是单位法向量，则Ⅱν(u)=〈Ⅱ(u)，ν〉是M与u，ν所张平面相交而成的平面曲线σ在点p的曲率．
c)若s是光滑法向量场，则ν(s)是微分ds在法丛v(M)上的正交投影．
Ⅱν=〈Ⅱ，v〉称为沿v方向的第二基本形式，对应于Ⅱν的自对偶算子Av称为M沿v方向的形状算子．
陈省身在欧氏微分几何上的工作主要是研究子流形的整体几何与其局部不变量之间的关系．他在这方面写了多篇重要论文，因篇幅所限这里只提出下面两项：
(1)极小曲面
因为Rn中子流形的面积的第一变分是第二基本形式的迹，所以当tr(Ⅱ)=0时称Rn的子流形M为极小子流形．用Gr(2，n)表示Rn中所有2维子空间形成的流形(称为格拉斯曼流形)．Rn中曲面M的高斯映射G是从M到Gr(2，n)的映射，它把点x∈M映到M在x的切平面G(x)．Gr(2，
面(把Rn中的2维平面V映为由e1+ie2张成的复直线，其中(e1，e2)是V的单位正交基底)．这样，Gr(2，n)有复结构．另一方面，Rn中的有向曲面通过它的诱导黎曼度量有一个共形结构，因而也有一个复结构．陈省身在[1—79]中证明：Rn中的曲面是极小的充分必要条件是其高斯映射G是反全纯的．此定理在n=4时由平尔(M．Pinl)所证，它是将极小曲面与奈望林纳(R．Nevanlinna)、H．韦尔、阿尔福斯(L．V．Ahlfors)的值分布理论联系起来的出发点．伯恩斯坦定理是极小曲面论的基本结果之一，它断言：在R3中定义在整个R2上的极小图z=f(x，y)必是一张平面．注意到一个完整的图的高斯映射的象必落在半球面内，故奥塞曼(R．Osserman)把伯恩斯坦定理推广为：若R3中一个完备的极小曲面的高斯映射的象在球面上不是稠密的，则该极小曲面必为平面．陈省身在[1—79]中利用波莱尔(E．Borel)的经典定理把伯恩斯坦-奥塞曼定理推广成Rn中非平面的极小曲面的高斯映象的密度定理，更细致的密度定理是在陈省身与奥塞曼的合作论文[1—86]中建立的．
根据卡拉比(E．Calabi)关于球面内极小曲面的工作，陈省身在[1—96]中对于子流形的密切空间作了一般性的叙述．他证明：若在空间型中给定一个极小曲面，则存在整数m，使得m阶密切空间沿曲面是平行的；同时给出了完全局部不变量组及其关系．最后得到与卡拉比类似的结果：若M是常曲率为c的空间型内的极小球面，且它的高斯曲率是常数K，
(2)紧贴浸入和紧套浸入
在1929年，费恩雪尔(W．Fenchel)证明：若α(s)是R3中一条简单闭曲线，s是弧长参数，k(s)是其曲率函数，则∫｜k(s)｜ds≥2π，且等式成立的充分必要条件是α为平面凸曲线．法雷(I．Fary)和米尔诺(J．Milnor)证明，若α是打结的，则上述积分必不小于4π．
在[1—62]和[1—66]中陈省身和拉瑟夫(R．K．Lashof)将费恩雪尔定理推广到Rn中的子流形．设f：M→Rn是紧致m维流形M在Rn中的浸入，v1(M)是M的单位法球丛，dv为v1(M)上的体积元．设N∶v1(M)→Sn-1为法映射，即它把点x∈M上的单位法向量v映为从原点引出的、平行的单位向量N(v)．da为Sn-1的体积元，则李普希茨-基灵曲率G由方程N*(da)=Gdv来定义，即G(v)是M沿单位法向量v的形状算子Av的行列式的绝对值．浸入f的绝对全曲率τ(M，f)是指N的象集的体积，即
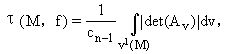
其中cn-1是Sn-1的体积．
在[1—62]中，陈省身和拉瑟夫证明τ(M，f)≥2，且等式成立的充要条件是M为Rn中一个(m+1)维仿射空间里的凸超曲面．在[1—66]里，他们进一步得到：M的贝蒂数之和是τ(M，f)的一个下界．
令τ(M)是M的所有浸入的绝对全曲率的下确界．如果浸入f：M→Rn满足τ(M，f)=τ(M)，则称f是紧贴的．紧贴浸入成为子流形几何重要的研究领域，近年来有许多有趣的发展．一个重要的发展是凯珀(N．H．Kuiper)用莫尔斯理论重述紧贴性概念．紧致流形M的莫尔斯数γ是指M上非退化莫尔斯函数的临界点个数的下确界．凯珀证明τ(M)=γ，且子流形M在Rn中是紧贴的充要条件是非退化的高度函数恰有γ个临界点．另一个重要发展是班科夫(T．F．Banchoff)和卡特(S．Carter)-韦斯特(A．West)引进的紧套浸入．Rn中的子流形M称为紧套的，如果每个非退化的欧氏距离函数有γ个临界点，紧套浸入必是嵌入，并且是紧贴的．紧套性是保角变换下的不变性质．因此经过球极投影总是可以假定紧套子流形是在球面上的．平卡尔(U．Pinkall)证明：Rn中围绕子流形M的半径为ε的管状超曲面Mε是紧套的充要条件是M为紧套的．由此可得两个结果：Sn中紧套超曲面的平行超曲面仍是紧套的；研究紧套子流形只须研究紧套超曲面．因为李球群(把球面映为球面的切触变换群)是由保角变换和平移生成的，故紧套性在李球群下不变．注意到Sn中子流形M的管状超曲面Mε是Sn的切球丛的切触流形的浸入勒让德子流形，故紧套性实际上可以对于Sn的单位切球丛的切触流形的勒让德子流形来定义．在[1—143]中陈省身和赛西尔(T．Cecil)把这个概念确切地叙述出来，并且引进李球群几何中的一些微分几何概念．虽然已有许多紧贴及紧套的例子和结果，但是许多基本问题尚未解决．例如：哪些紧致流形可以紧贴或紧套地浸入到欧氏空间中去？哪些是李球群几何的完全不变量？等等．
(转自《中国现代数学家传》)