陈省身 －广义的高斯-邦尼公式
(转自《中国现代数学家传》)
R.帕勒 滕楚莲
作者简介 R．帕勒(Richard Palais)1931年出生于美国麻省凌县(Lynn，Massachusetts)．哈佛大学博士(1956)．现为勃朗蒂(Brandeis)大学教授．
滕楚莲（Chuu-Lian Terng） 1949年出生于台湾花莲．美国勃朗蒂大学博士(1976)．现任美国加州大学教授．
本文的材料主要取自：《陈省身论文选集》(S．S．Chern，Se-lected papers，vol．1—vol．4，Springer-Verlag，1978—1989)；《陈省身文选——传记、通俗演讲及其它》(科学出版社，1989)；以及作者与陈省身本人的多次谈话．文中，记号[1—25]，[1—30]等分别表示文献中所列的陈省身的出版物的序号．
陈省身
广义的高斯-邦尼公式
几何学家通常把局部问题与整体问题划分得壁垒分明，且认为只有整体问题才更重要．而陈省身认为在几何学上似乎南辕北辙的两个方面的研究须同时进行．他觉得若不了解局部理论(即等价问题)则整体问题就无从下手，反过来找到了完全不变量组则整体问题的解决也快了．下面将简述陈省身对几何学的这种看法的形成过程，它既有趣又有启示性，而且涉及到他的最重要、最令人激奋的研究工作：给广义的高斯-邦尼公式一个内蕴证明，进而引入复向量丛的示性类，即现在所称的“陈示性类”，并给出陈示性类的一个漂亮的、用曲率张量写出的公式．示性类的局部性质是曲率，其整体性质基于映射的同伦性，两者交织便成为几何学的基本工具．
二维紧致流形上的高斯-邦尼公式当然是经典微分几何的一个高峰．霍普夫曾说：“推广此公式到高维紧致流形上去是几何学中极其重要而困难的问题．”此公式把紧致曲面M上的最基本的不变量——欧拉示性数χ(M)与曲面的微分几何的最基本不变量——高斯曲率K联系在一起：
出的、用活动标架观点的新证明是极自然的，而且具有推广到高维情形的潜力．
要解释陈省身的证明，这里先讨论一般的n维黎曼空间上的活动标架，然后再考虑n=2的特例．设M上有一个有向的黎曼结构，即一个SO(n)-结构．因它的李代数L(SO(n))由全体n阶反对称矩阵所组成，在单位正交切标架构成的SO(n)-主丛F(M)上有n个一次微分形式(ωi)及列维-奇维塔联络形式(ωij)(ωij=-ωji)满足下列方程：dωi=∑ωij∧ωj．黎曼曲率张量在正交标架(ωi)下的系数为Rijkl，即Ωij=∑Rijklωkωk∧ωl．当n=2时，L(SO(2))是一维李代数，ω11=ω22=0，ω12=-ω21，所以只有一个曲率方程dω12=-Ω12=-R1212ω1∧ω2．显然，在每个纤维π-1(x)上R1212是常数，其值是M的高斯曲率K(x)．设(θ1，θ2)是M上的单位正交余切标架，则M的面积元为dA=-θ1∧θ2，且
π*(KdA)=dω12． (*)
陈省身在[1—136]中说：“公式(*)包含了曲面的全部局部几何，也可推演出整体几何性质．仔细考虑过之后，容易看出(*)是高斯-邦尼公式的证明的要义，而且n维流形上的高斯-邦尼公式的证明也是从这个想法发展出来的．”陈省身看出：曲面上的二次微分式必是闭的，被π拉回到F(M)仍然是闭的．但是除了M是环面的情形，KdA绝不是恰当微分形式．然而(*)式表明它在F(M)上是恰当的．这是(*)式的一个意想不到的性质．这种在M上非恰当的微分形式拉到M的主丛的全空间上成为恰当微分形式的现象称为“超度”，这个概念在陈省身的证明中起极重要的作用．
根据初等拓扑学，在闭黎曼流形M关于定点p的补集M′上存在光滑的单位向量场e1，这个向量场在p点的指标是χ(M)．令e2是M′上与el正交的单位向量场，且(e1，e2)与M的定向一致．令θ是对偶标架场．因π·θ是M上的恒同映射，故d(θ*(ω12))=θ*(dω12)=KdA，于是
令Mε为M上去掉以p为心、以ε为半径的球所得的补集，Sε=Mε，于是
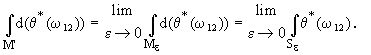
设xk为M在p点附近的坐标系，(ê1 ， ê2)为将自然标架正交化得到的正交标架场，命α(x)=∠(e1(x)，ê1(x))，则e1在p点的指标等于
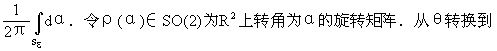
θ的度规变换是g∶U→SO(2)，g(x)=ρ(α(x))，且θ*(ω12)=dα+θ*(ω12)．所以
由于第二项的被积函数是连续的，当ε→0时该项趋于零；第一项正是所需的值．这就证明了高斯-邦尼公式．
现在我们考虑n维可定向黎曼流形，并且解释从2维高斯-邦尼公式发展出来的绝妙的结果．
如何用M的黎曼度量造出M上典型的微分式是一个基本问题．在其主丛的全空间F(M)上这是很容易的，只要取曲率形式Ωij的多项式即可．但是由此造出的微分形式Λ不一定是M上的微分形式经过π拉回来的，即在M上不一定存在微分形式λ，使得Λ=π*λ．
n阶反对称矩阵，使它的第(i，j)个元素为Xij(i＜j)．取g∈SO(n)，则矩
ad(g)X=gXg-1
(ad(g)P)(X)=P(ad(g)X)，
这就定义了SO(n)在
上的伴随作用．令
ab为中的SO(n)的伴随作用下的不变多项式构成的子环．
因曲率形式Ωij是二次微分形式，在外积下彼此是可换的，故当P∈时，可用Ω代替X．若P是d次齐次多项式，则P(Ω)是F(M)上的2d次外微分形式． 
个截面．令Ψ=θ*(Ω)，则θ*(P(Ω))=P(θ*(Ω))=P(Ψ)．若θ是由θ经过度规变换g∶U→SO(n)得到的，则由前述可知Ψ=ad(g)Φ，P(Ψx)=P(ad(g(x))Ψx)=(ad(g(x))P)(Ψx)，所以P(Ψ)只是在M上局部可定义的，且与θ的选择有关．如果P∈ab，则P(Ψ)就成为在整个M上定义的微分形式，且与θ的选择无关，因此P(Ψ)由等式π*(P(Ψ))=P(Ω)唯一确定．
将高斯-邦尼公式推广到高维情况的方法有很多，但是最自然、最合理的方式是对每个n维紧致黎曼流形给定一个相伴的n次微分式λ，使
可知χ(M)=0，所以我们只考虑n=2k(但是奇维有边流形的公式是有趣的)．按上述讨论，我们应该找一个k次齐次伴随不变的多项式P，取λ=P(Ψ)．由SO(n)的不变量理论，P有一个自然的候选者，即满足条件[PF(X)]2=det(X)的唯一的伴随不变多项式Pf(称为Pfaffian)．陈省身首次看出高斯-邦尼公式的被积式是Pf．在此之前，艾伦多弗(C．Allendoerfer)和费恩雪尔已各自证明了高维的高斯-邦尼公式，其被积式是一堆曲率张量的组合，而且证明是外蕴的，即假定M可以等距地浸入到欧氏空间(艾伦多弗及韦伊的证明只须假设M可局部等距浸入到欧氏空间即可，所以他们把高斯-邦尼公式推广到解析度量的情形)．然而陈省身在[1—25]中给出的是一个内蕴证明，是前面所介绍的曲面情形的证明的推广．
令S(M)为M的切球丛，γ∶S(M)→M为自然投影．对F(M)中任一元素θ，令e1(θ)代表θ的对偶标架的第一个向量，则e1是从F(M)到S(M)的丛同态，且π=γ·e1．命λ=pf(Ψ)，Λ=γ*(λ)，则陈省身在[1—25]中首次证明了Λ的超度引理，即在S(M)上找到一个(n-1)次微分式
，使得d=Λ，且给出的一个显式表示．与曲面情形的做法类似，令M′为M上去掉一点p的补集，ζ为S(M)在M′上的光滑截面，则得
因是具体构造出来的，陈省身可以算出上面等式右端的值，它恰好是一个通用常数乘以M的欧拉示性数．
通常，数学家对于给出旧定理的新证明的评价不及给出新定理来得高，然而[1—25]却是例外．因为n维高斯-邦尼公式的早期证明几乎是条死胡同，而陈省身的内蕴证明却是进入示性类的秘门钥匙．
(转自《中国现代数学家传》)