陈省身 － 示性类

(转自《中国现代数学家传》)

R.帕勒　　 滕楚莲

作者简介 R．帕勒(Richard Palais)1931年出生于美国麻省凌县(Lynn，Massachusetts)．哈佛大学博士(1956)．现为勃朗蒂(Brandeis)大学教授．

滕楚莲（Chuu-Lian Terng） 1949年出生于台湾花莲．美国勃朗蒂大学博士(1976)．现任美国加州大学教授．

本文的材料主要取自：《陈省身论文选集》(S．S．Chern，Se-lected papers，vol．1—vol．4，Springer-Verlag，1978—1989)；《陈省身文选——传记、通俗演讲及其它》(科学出版社，1989)；以及作者与陈省身本人的多次谈话．文中，记号[1—25]，[1—30]等分别表示文献中所列的陈省身的出版物的序号．

　　陈省身 1911年10月28日诞生于浙江嘉兴．美国科学院院士、南开数学研究所所长．微分几何、拓扑学．

　　

示性类

　　本文中一再出现的余标架丛F(M)是G-主丛的重要例子．主丛的定义和研究在30年代末已经开始，但是到40年代几何学家和拓扑学家才看清它的重要性，并进行全面的研究．到40年代末，完美的分类工作已经完成，并发展出一套丛上的“示性类”理论，示性类的观念的重要性在20世纪后半叶是无可言喻的．其实，分类问题是主丛的等价问题，而示性类是等价问题的不变量．为解释陈省身在这方面的贡献，我们先叙述一些背景材料．

　　G-主丛的理论与G的极大紧子群的主丛理论是相同的，故我们设G是紧李群．若仿紧空间P上有一个G的右作用，则称P为G空间．设g∈G，R_g表示g在P上的右作用给出的变换，即R_g(x)=xg．若当g≠e时R_g在P上没有不动点，则称G在P上的作用是自由的．所谓G-主丛是纤维化π：P→X，使得P是自由的G空间，且X是P的G轨道空间P/G．所以G-主丛在点x的纤维是一条G轨道．P称为主丛的全空间，并常以P代表G-主丛．若映射σ∶X→P满足π·σ=id，则称σ为P的一个截

π(x，h)=x，则称此G-主丛为平凡丛．映射x→(x，e)显然是此平凡丛的截面．反之，若一个G-主丛存在一个截面，则该主丛必是平凡的．令Bndl_g(X)表示X上的G-主丛P的等价类[P]构成的集合．

　　设π∶P→X是一个G-主丛，f：Y→X是连续映射，用f^*(P)表示由f生成的诱导丛，它的全空间={(p，y)∈P×Y：π(p)=f(y)}．G的右作用定义为R_g(p，y)=(R_g(p)，y)．容易看出f^*把等价丛诱导为等价丛，所以f^*可看作从Bndl_g(X)到BndlG(Y)的映射．若π∶P→X是G-主丛，则π^*(P)是P上的G-主丛，称为G-主丛P的“平方”．显然，映射p→(p，p)给出了π^*(P)的一个截面，所以π^*(P)是平凡丛．下面将说明这个简单的观察是藏在“超度”背后的秘密．

　　主丛理论的第一个重要事实是：给定映射f：Y→X，则映射f^*∶Bndl_g(X)→Bndl_g(Y)只与f的同伦类[f]有关．用范畴的语言来说就是：Bndl_g()是拓扑空间与映射同伦类的范畴到集的范畴的反变函子．上同调群H^*()也是一个反变函子．示性类则是从Bndl_g()到H^*()的一个自然的变换．当然这种花巧的语言并非是必须的．直接地说，所谓示性类c是一个函数，它对任意一个空间X上的每一个G-主丛P都指定了H^*(X)中的一个元素c(P)，并且对于任意一个连续映射f：Y→X满足c(f^*(P))=f^*(c(P))．用Char(G)表示所有G-主丛的示性类构成的集合．因为H^*(X)是一个环，故Char(G)也是一个环．示性类的主要问题是确切地了解这个环．平凡G-主丛可以看成由一个常值映射诱导出来的，所以它的所有示性类为零(除了单位元示性类)．一般说来，所有示性类都相等是G-主丛等价的必要条件．

　　G-主丛∶→Z称为通用G-主丛，如果任意给定X上的G-主丛P，必有唯一的映射f：X→Z的同伦类[f]，使得[f^*()]=[P]．意想不到的是这种通用G-主丛是存在的，并且有多种构造方法．若取U_g→B_g为一个通用G-主丛，用[X，B_g]表示从X到B_g的映射同伦类的集合，则Bndl_g(X)可以与[X，B_g]等同，因此B_g称为G的分类空间．此外， ^G 的全空间是可缩的，B_g的同伦型不依赖于通用丛的取法．若π∶P→X是一个G-主丛，则存在映射h∶X→B_g，使得[h^*(_g)]=[P]，且[h]是唯一的，映射h称为分类映射．

　　现在可以容易地给出示性类问题的解，即Char(G)=H^*(BG)，且若c∈H^*(B_g)，则c(P)=f^*(c)，其中f是P的分类映射．

　　以上是从1935年到1950年间主丛发展的要点，主要贡献者包括陈省身、埃瑞斯曼(C．Ehresmann)、霍普夫(H．Hopf)、费尔德保(J．Feldbau)、庞特里亚金(Л．С．Понтрягин)、斯廷罗德(N．E．Steenrod)、施蒂费尔(E．Stiefel)及惠特尼(H．Whitney)．上述理论虽然简单优美，但太抽象，在真要写出Char(G)时并不是真有用的．同时对于由几何问题产生的主丛的示性类计算也用不上，因为找分类映射并非易事．下面我们要讨论陈省身如何建立具体的分类空间，更重要的是如何用主丛上联络的曲率计算示性类的微分形式代表．

　　令V(n，N+n)代表施蒂费尔流形，即Rⁿ⁺ⁿ中所有正交n-标架e=(e₁，…，e_n)的空间．V(n，N+n)是自由的O(n)空间，在e的轨道是由e₁，…，e_n所张的子空间上所有的正交基，故轨道空间正是格拉斯曼流形Gr(n，N+n)．投影π：V(n，N+n)→Gr(n，N+n)是O(n)-主丛．在40年代初期，斯廷罗德和惠特尼已证明：若N≥k+1，则此主丛是所有维数≤k的紧多面体上O(n)-主丛的通用主丛．在[1—43]陈省身与孙以丰将此结果推广到k维紧拓扑空间．若要得到B_o(n)只要取归纳极限π∶V(n，∞)→Gr(n，∞)即可．将实数换为复数或四元数体，他们也对U(n)-主丛和Sp(n)主丛证明了类似的结果．若G是任一紧群，则取正交表示G→O(n)，于是V(n，N+n)成为自由G空间，V(n，N+n)/G是维数≤k的紧致拓扑空间的通用G-主丛．

　　格拉斯曼流形是做分类空间的好模型，因为它的上同调群已用代数的或几何的方法算出了．因而陈省身知道在Char(SO(n)中有一个欧拉类e．若M是n维紧致流形时，则e(F(M))作为Hⁿ(M)中的元素作用在基本类M上时便得到χ(M)．高斯-邦尼公式可以解释为：λ=Pf(Ψ)是e(F(M))作为德拉姆上同调类的代表．这也启发陈省身去寻找一般示性类的微分形式代表．此时正是1944—1945年陈省身在普林斯顿的时期，他的朋友韦伊鼓励他，并且经常与他讨论此问题．

　　寻找SO(n)示性类的微分形式代表看上去似乎是一个自然的问题，然而陈省身看清楚实格拉斯曼流形的上同调群非常复杂，而且有Z₂挠群，而此挠群用微分形式表达不出来；另外，陈省身从埃瑞斯曼的博士论文知道复格拉斯曼流形没有挠群，且舒伯特胞腔是以整数Z为系数的同调群的基；所以根据德拉姆定理，所有B_U(n)的示性类可以由闭微分形式为代表．但要算某个U(n)-主丛P的示性类仍须知道P的分类映射，所以在实用上必须有一种从几何数据计算示性类的方法．下面将介绍陈省身的优美算法．

　　 设π∶P→M为流形M上的U(n)-主丛．P上的联络是在L(U(n))中

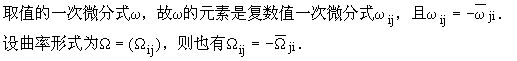
　　设^ab是L(U(n))上的伴随不变多项式的集合，若Q∈^ab，则Q(Ω)是由M上的唯一的一个微分形式Q(Ψ)诱导而来的．陈省身用比安基恒等式证明Q(Ψ)是闭的，故 [Q(Ψ)]∈H^*(M)．令ω′为P上另一个联络，Ω′是曲率形式，则得M上另一个微分形式Q(Ψ′)使得π^*(Q(Ψ))=Q(Ω′)．根据韦伊的一个引理，Q(Ψ′)与Q(Ψ)只差一个恰当微分式，所以(P)=[Q(Ψ)]=[Q(Ψ′)]是M上同一个上同调类，它与联络的取法无关，是一个示性类．

　　令h∶M′→M是光滑映射，P上M上的U(n)-主丛，ω是P上的联络，则P，ω及其曲率Ω均可经h自然地诱导到M′上．所以Q(h^*(P))=h^*(Q(P))．Q映至是由^ab到Char(U(n))的环同态．因为韦伊的引理，陈省身称此为韦伊同态，但是一般称它为陈-韦伊同态．

　　L(U(n))上的伴随不变多项式环^ab可以简单地写出来．令z为反埃尔米特n阶矩阵，σ_k(z)是det(z+tI)中t^n-k的系数，则σ_k(z)∈^ab．实际上，σ_k(z)只是z的特征值的k次对称函数，例如σ₁(z)=tr(z)，σ_n(z)=det(z)．若P(t₁，…，t_n)∈C[t₁，…，t_n](即变量t₁，…，t_n的复系数多项式环)，则P(σ₁(z)，…，σⁿ(z))∈^ab，且映射P(t₁，…，t_n)→P(σ₁(z)，…，σ_n(z))是从C[t₁，…，t_n]到^ab的环同构．再引用埃瑞斯曼关于格拉斯曼流形的同调群的结果，陈省身看出

　

　　　　

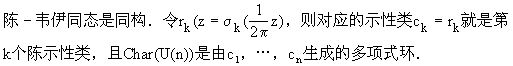
上，当r很大时示性类_r为零，所以是一示性类．希策布鲁赫(F．Hirzebruch)用形式幂级数定出许多示性类，陈省身用E(z)=trace

要作用．

　　陈省身也将上面关于U(n)-主丛的示性类的结果推广到一般的紧致李群， ^ab 仍与以复数为系数的Char(G)同构．但一般说来，B_g有挠群，故可能存在不能用微分形式表示的示性类．

　　在此后近20年陈省身未做示性类方面的研究，但在1974年他与西蒙斯(J．Simons)写了一篇在示性类方面极重要的文章[1—103]．该文对于主丛上的“超度”现象做了一个详尽的研究．令π∶P→M为G-主丛，ω，Ω如前所述．令Q是L(G)上l次齐次的伴随不变的多项式，则存在唯一的、定义在M上的2l次闭微分式Q(Ψ)，使得π^*(Q(Ψ))=Q(Ω)，并且它是同调类(P)∈H^2l(M)的代表．由于[Q(Ω)]=[π^*(Q(Ψ))]=[Q(π^*(Q(Ψ))]=Ψ(π^*(P))，且前面已说明P的平方π^*(P)是平凡的，故它的示性类必为零，因此Q(π^*(P))=0，Q(Ω)是恰当的．然后他们用Ω，ω确切地写出P上的一个(2l-1)次微分形式TQ(ω)，使得dTQ(ω)=Q(Ω)．TQ(ω)在丛及联络的诱导下是自然的(即TQ(f^*ω)=f^*(TQ(ω))等)．设2l＞n，则Q(Ω)=0，故TQ(ω)是闭的，[TQ(ω))]是H^2l-1(P)中的一个元素．当2l＞n+1时，他们证明[TQ(ω)]与ω的选择无关，称为从属示性类(the secondary char-acteristic classes)．而且当2l=n+1时，他们证明[TQ(ω)]确实与联络ω有关．

　　

项式．取Q=Q_2k-1，设P是M上的切标架丛，ω是黎曼结构的列维-奇维塔联络，他们证明[TQ(ω)]属于H^*(P)，并且它与黎曼度量的取法有关，而在黎曼度量的保形变换下是不变的．这是一个惊人的结果．这个不变量近来在物理学共形量子场论的表述中要用到．

　　另外，陈省身与博特(R．Bott)合作的论文[1—92]中讨论了n维复流形X上的全纯埃尔米特向量丛E的示性类及其超度．复流形上的微分形

究．这个理论与代数数论有密切关系，比斯穆特(J．M．Bismut)，吉勒特(H．Gillet)和索尔(C．Soule)有重要的发挥．

　　陈省身是享誉世界的数学家，尤其是在微分几何学及拓扑学方面做出了非常杰出的重要贡献．他被公认为20世纪后半叶杰出的几何学家．正如20世纪前半叶的几何学带有E．嘉当的消除不掉的印记一样，在过去50年中所描绘的几何学留下了陈省身的硕大的印章．除了他的科学成就赢得的崇敬和赞誉之外，无数的同事、学生和朋友对他怀有深厚的感情和敬意．这反映了他的人生的另一个方面——陈省身总是对他人显示友谊、热情和关怀，他始终如一地像致力于自己的研究工作那样来帮助年轻的数学家充分发展他们的潜能．

(转自《中国现代数学家传》)